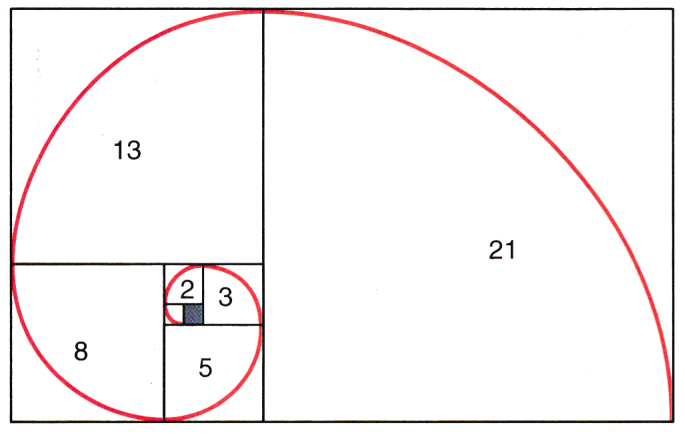
Wenn man Quadrate unterschiedlicher Größe spiralförmig aneinander legt, so das in jedem Schritt wieder ein Rechteck entsteht, so ergeben sich für die Seitenlängen der Quadrate die Fibronaccizahlen.

| zurück Home | Fibonacci - Zahlen | |||
| allgemeines | 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377 .... |
 Wenn man Quadrate unterschiedlicher Größe spiralförmig aneinander legt, so das in jedem Schritt wieder ein Rechteck entsteht, so ergeben sich für die Seitenlängen der Quadrate die Fibronaccizahlen. | ||
| Definition | Jede Zahl ist die Summe ihrer zwei Vorgängerinnen. | |||
| Perioden | letzte Ziffer | 0 , 1 , 1 , 2 , 3 , 5 , 8 , 3 , 1 , 4 , ... | Wiederholung nach 60 Zahlen. | |
| letzte 2 Ziffer | 00 , 01 , 01 , 02 , 03 , 05 , 08 , 13 , ... | Wiederholung nach 300 Zahlen. | ||
| letzte 3 Ziffer | 000 , 001 , 001 , 002 , 003 , 005 , 008 , 013 , ... | Wiederholung nach 1500 Zahlen. | ||
| letzte 4 Ziffer | 0000 , 0001 , 0001 , 0002 , 0003 , 0005 , 0008 , 0013 , ... | Wiederholung nach 15.000 Zahlen. | ||
| letzte 5 Ziffer | 00000 , 00001 , 00001 , 00002 , 00003 , 00005 , 00008 , 00013 , ... | Wiederholung nach 150.000 Zahlen. | ||
| Teilbarkeit | Benachbarte Fibonaccizahlen | stets teilerfremd. | 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 | |
| jede 3. Fibonaccizahl | durch 2 teilbar | 2, 8, 34, 144 | ||
| jede 4. Fibonaccizahl | durch 3 teilbar | 3, 21, 144 | ||
| jede k-te Fibonaccizahl | durch k-1 teilbar | |||
 |
||||
Impressum Zuletzt geändert am 13.03.2017 19:13