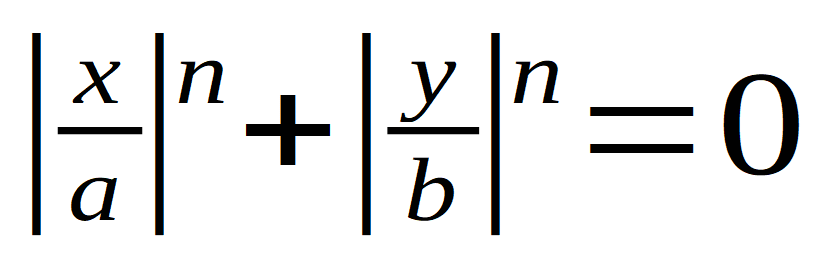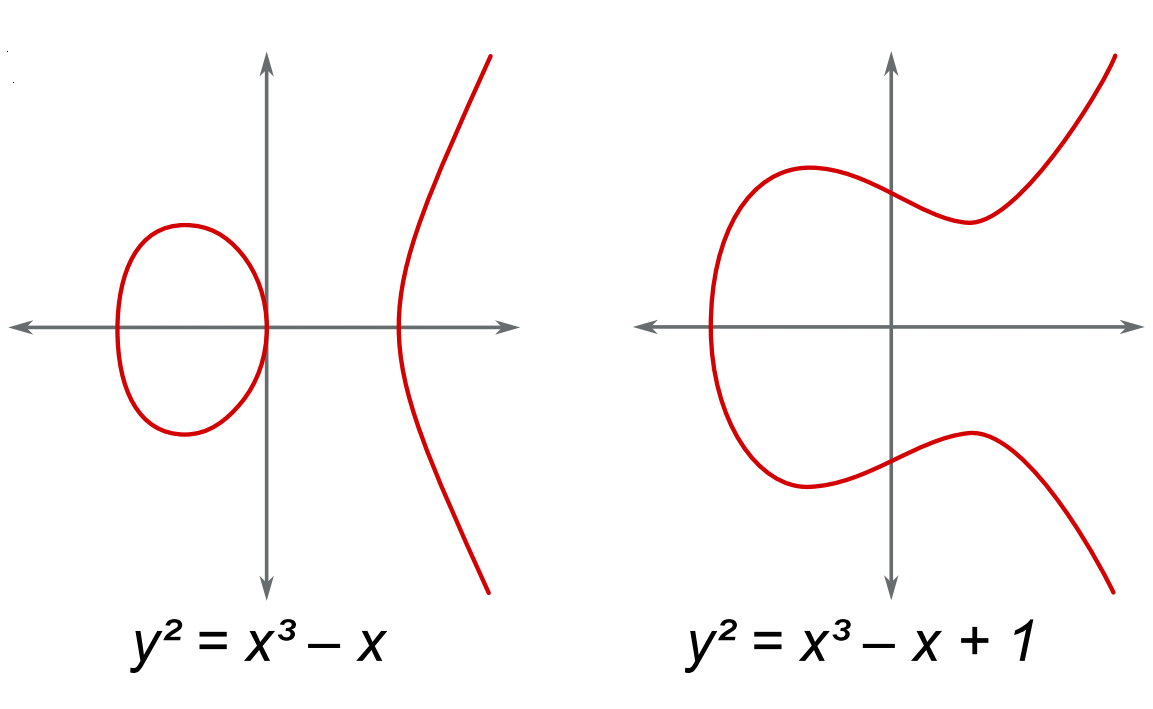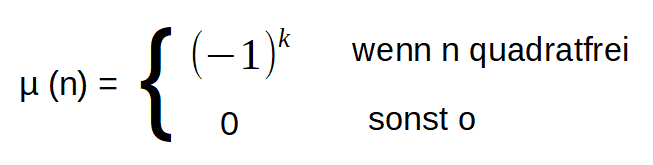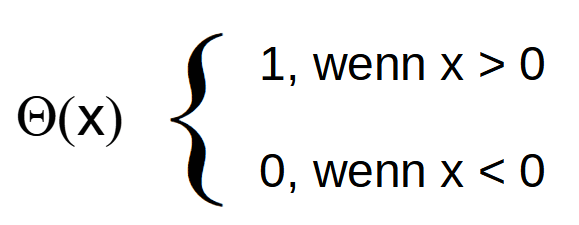| zurück
Home |
Funktionen |
| allgemeines |
|
| Stetigkeit |
Eine Funktionen, die keine Sprünge aufweist. Z.B. Sinusschwingung. |
Die Funktion, welche die Menge an Geld auf einem Konto beschreibt, ist nicht stetig, weil sie plötzlich von einem Wert zu einem anderen springen kann. |
| Differenzierbarkeit |
Differenzierbarkeit ist die Abwesenheit von Knicken. |
Eine Funktion ist differenzierbar in einem Punkt, wenn sie in diesem Punkt eine Tangente hat. |
Die Steigung dieser Tangente (die Ableitung der Funktion) beschreibt die lokale Änderungsrate der Funktion. |
| Extrema |
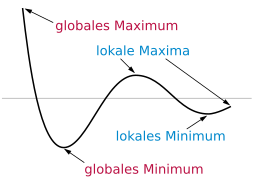
Bildquelle: Georg-Johann, Public domain, via Wikimedia Commons |
|
| Sekante |
Die Sekante (blau) schneidet die Funktion f(x) (rot) in den Punkten P und Q.
 |
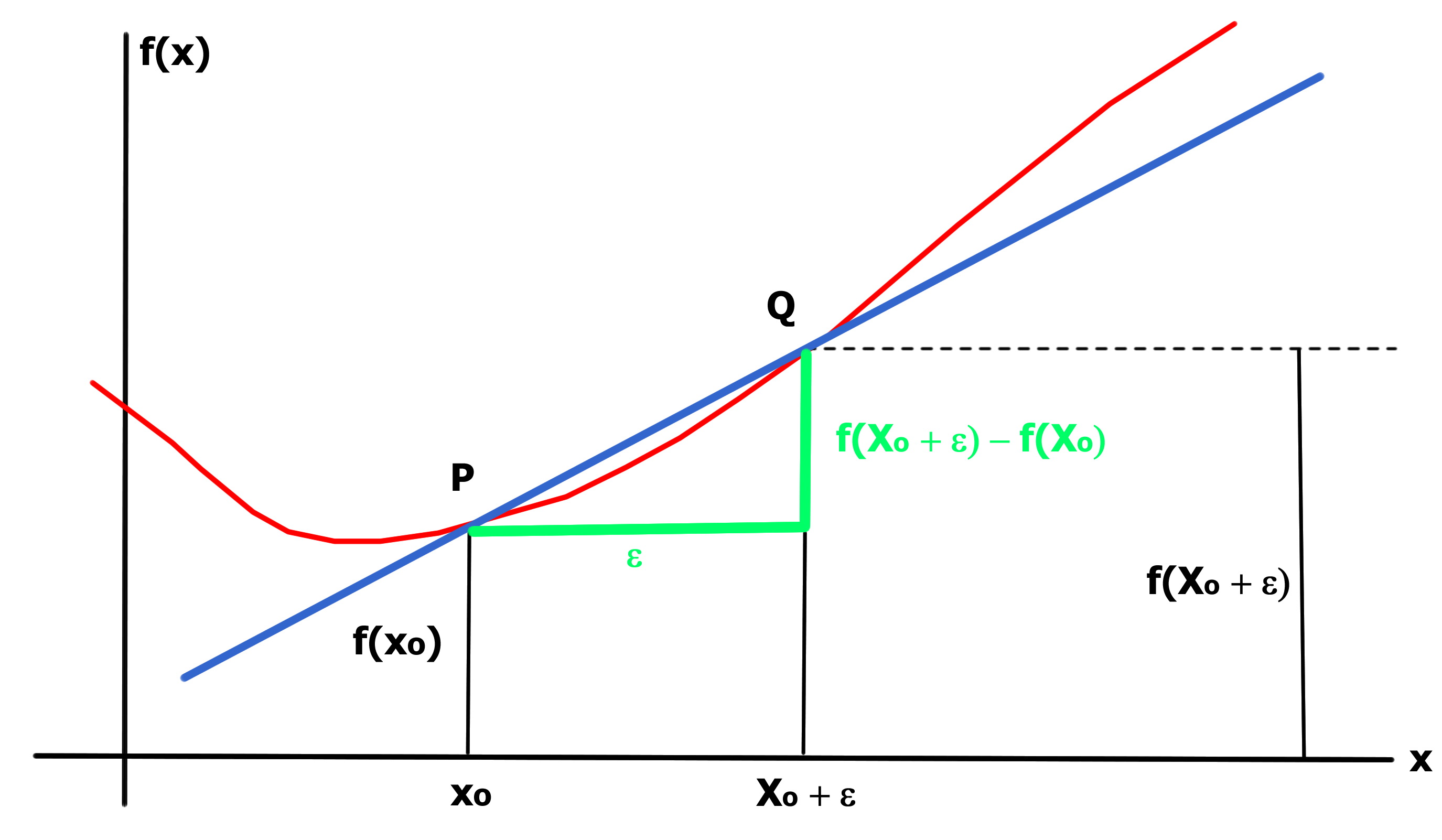| polynomiale Gleichung |
f(x) = a1 x + a2 x2 + … + an xn |
| trigoniometrische Funktionen |
Sinus
 |
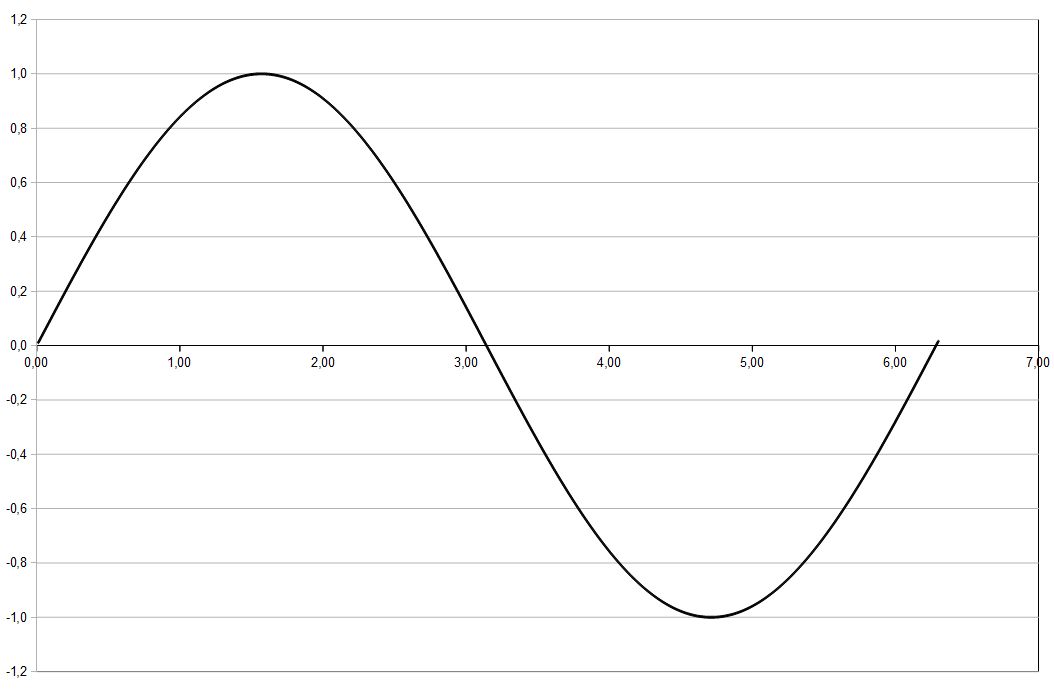Cosinus
 |
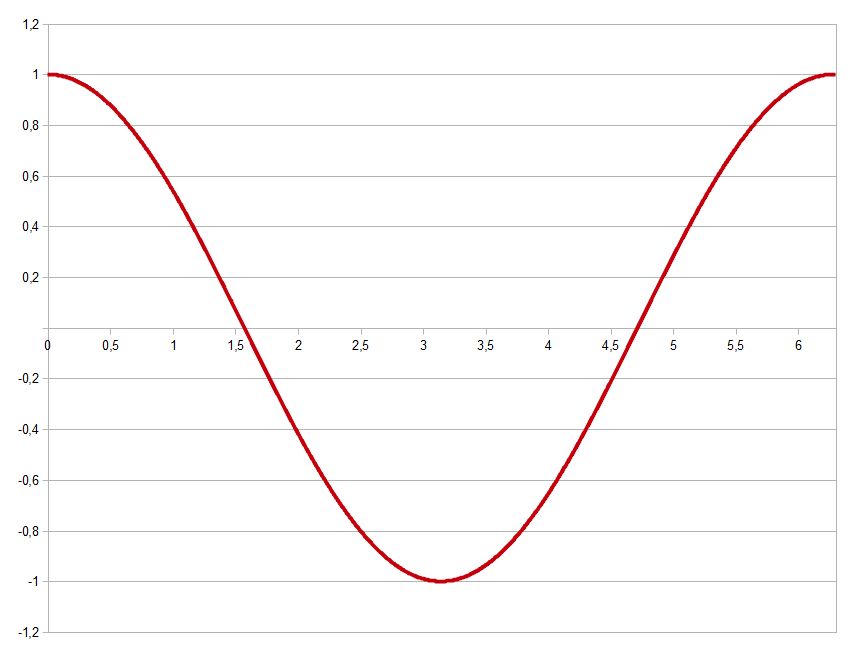Tangens
 |
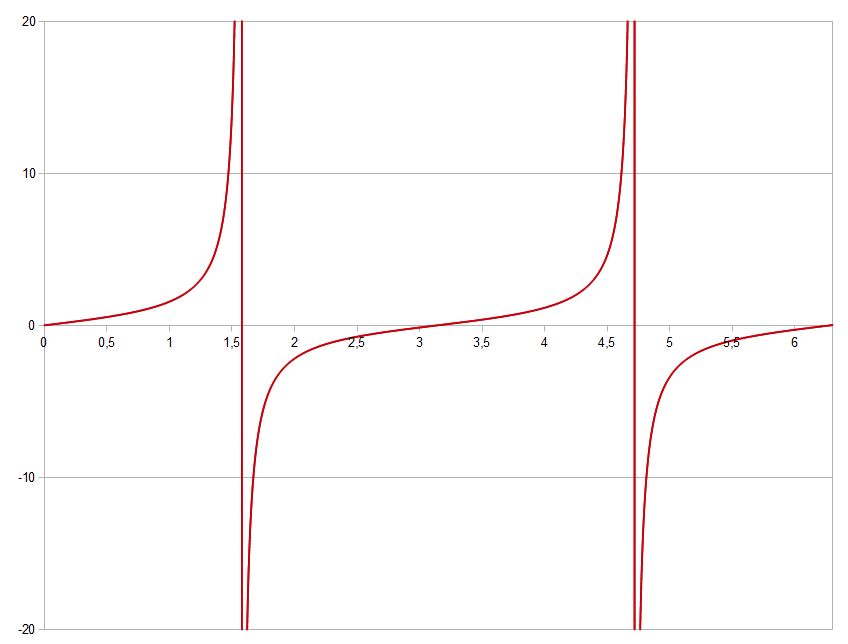| Lamé-Funktion |
 |
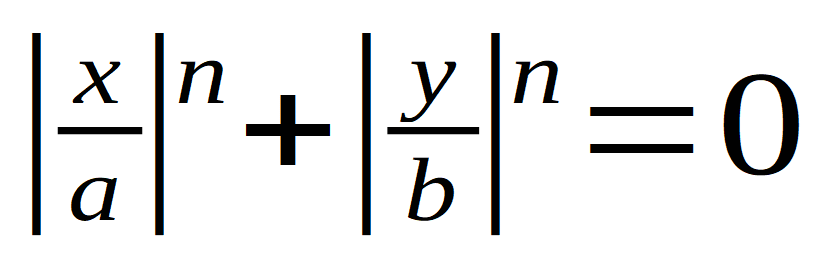"Superellipse"
a,b: Halbachsen
n = 2: Ellipse
n >> 2: Rechteck |
Ellipse
 |
| Elliptische Kurven |
y2 = x3 + ax + b |
 |
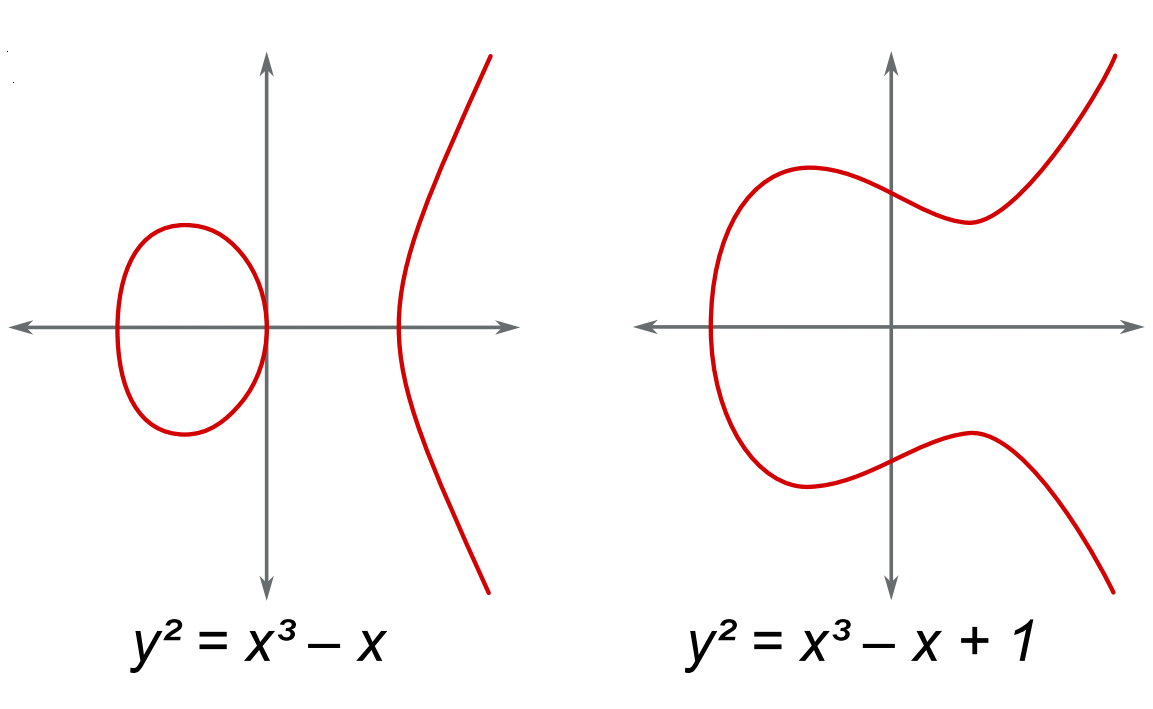| Möbius-Funktion |
 |
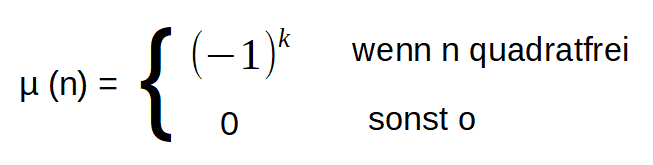n: natürliche Zahlen > 0
µ: kann nur -1 oder +1 oder 0 sein
k: Zahl der Primzahlen, die in n enthalten sind
Wenn eine Primzahl 2x enthalten ist (= Quadrat, z.B. 4, 8, 9, 12), so wird µ = 0. |
| Lissajous-Figuren |
Entstehen durch harmonische Schwingungen ungleicher Frequenz. |
x = A1 sin (ω1t + Φ1)
y = A2 sin(ω2t + Φ2) |
Die Funktion ist periodisch, wenn ω1 : ω2 ein ganzzahliges Verhältnis bilden.
Bildquelle: Urs Hartl, CC BY-SA 3.0 , via Wikimedia Commons |
A1, A2: Amplitude
ω1t: Kreisfunktion
Φ1: Phase |
| Cardioide |
Ein äußerer Kreis rollt auf einem inneren Kreis.
Der äußere Kreis enthält einen festen Punkt.
Dieser beschreibt eine Cardioide (rote Linie).
Rollt ein kleiner Kreis im Innern eines größeren Kreises,
so beschreibt ein fester Punkt auf dem kleinen Kreis eine eine Deltoide (blaue Linie).
Von Greg Egan [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)] |
| Lemniskate |
Bildquelle: Urs Hartl, CC BY-SA 3.0 , via Wikimedia Commons |
| Partitierungs-Funktion |
p(n) |
p gibt die Anzahl der Möglichkeiten an, die positive ganze Zahl n in positive ganze Summanden zu zerlegen. |
Z.B. lässt sich die Zahl 4 als 1 + 1 + 1 + 1, 1 + 1 + 2, 2 + 2, 1 + 3 oder als 4 schreiben. p(4) = 5. |
p(5) = 7
p(9) = 30
p(100) = 190.569.292 |
| diophantischen Gleichungen |
x2 + d * y2 = 1 |
nur Lösungen mit ganzen Zahlen. |
Lösung z.B. x = 3; d = 2; y = 2 |
| Heaviside-Funktion |
 |
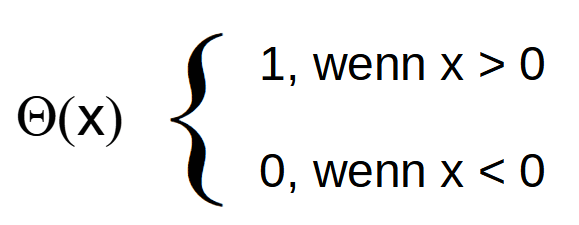Teil von |
Mathematik |
| Quellen |
1.) Abramowitz M, Stegun IA:
Handbook of Mathematical Functions.
Dover Publications, New York, 1965
|
 |
|
