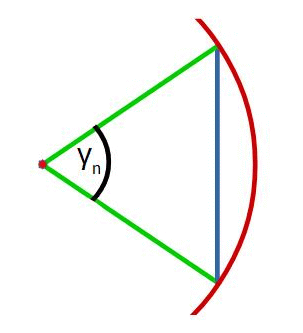
γn ist der Öffnungswinkel des Bestimmungsdreiecks
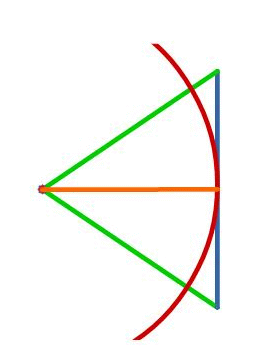
r * sin (γn /2) = s / 2
r * cos (γn /2) = g
s: Seitenlänge g: Radius des Innkreises

| zurück Home | regelmäßiges, gleichseitiges Vieleck | |||
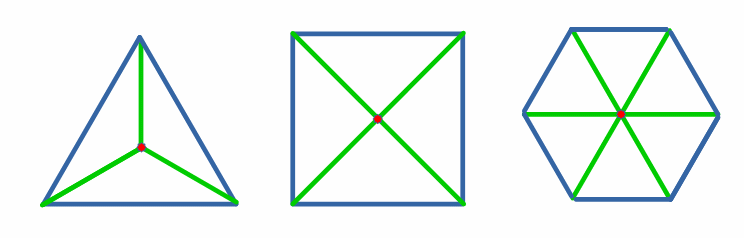
| allgemeines | Gleichseitige Vielecke mit n gleichen Seiten der
Länge s (blau) lassen sich in n gleichschenklige Dreiecke (grün) mit dem Mittelpunkt M (rot) zerlegen. | |||
| Bestimmungsdreieck | Die Seiten des Dreiecks r (grün) sind immer der Radius des Umkreises(braun).
γn ist der Öffnungswinkel des Bestimmungsdreiecks  |
Die Winkelhalbierende g (orange) ist der Radius des Innkreises. r * sin (γn /2) = s / 2 r * cos (γn /2) = g | ||
| Seitenwinkel α | Die n Seiten der Länge s bilden den Winkel: | α = (2 n -4) * 90° / n | ||
| Öffnungswinkel α | Die gleichschenkligen Dreiecke bilden den Winkel: | γ = 360° / n | ||
| Fläche A | A = n * s * g / 2 | n: Zahl der Seiten s: Seitenlänge g: Radius des Innkreises |
||
 |
||||
Impressum Zuletzt geändert am 02.10.2019 16:45