zurück Home	Folgen, Reihen
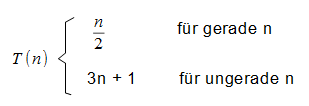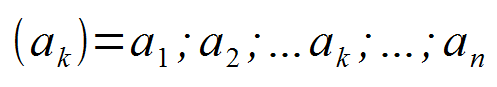
allgemeines		ak: Bilder, Glieder der Folge k: Urbilder, Indizes der Glieder a1: Anfangsglied an: Endglied
Arten	endliche Folge unendliche Folge Differenzfolge Quotientfolge Partialsummenfolge positiv definite Folge negativ definite Folge alternierende Folge monoton wachsende Folge monoton fallende Folge konstante Folge
Geometrische Reihe	Eine geometrische Reihe ist die Summe von Potenzen mit steigendem Exponenten.	Die Summe konvertiert, wenn q < 1 und q > -1 ist, nach der Formel:	Wenn a0 = 1 und q = 1/2 ist, so konvertiert die Reihe mit dem Wert 2.
Euler-Mascheroni- Konstante		0,57721566490153286060…
Huygens - Reihe
Riemannsche Zetafunktion
Fibonacci - Zahlen	0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377 ....	Jede Zahl ist die Summe ihrer zwei Vorgängerinnen.
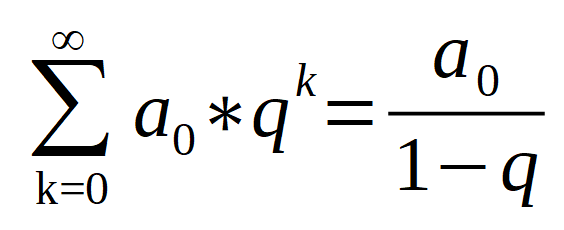
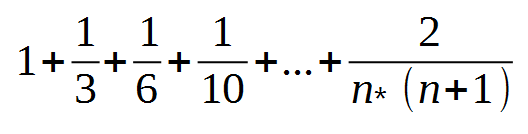
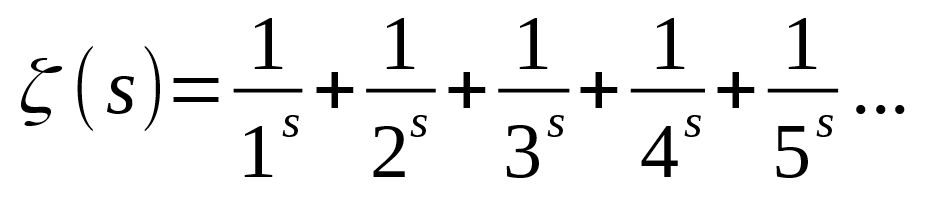
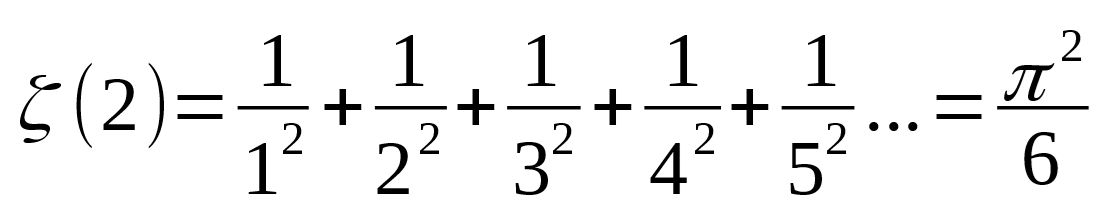
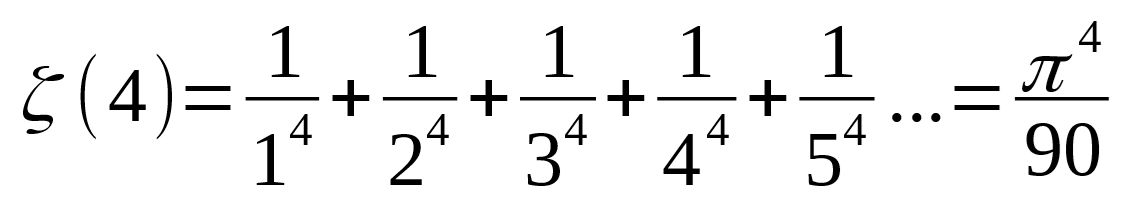
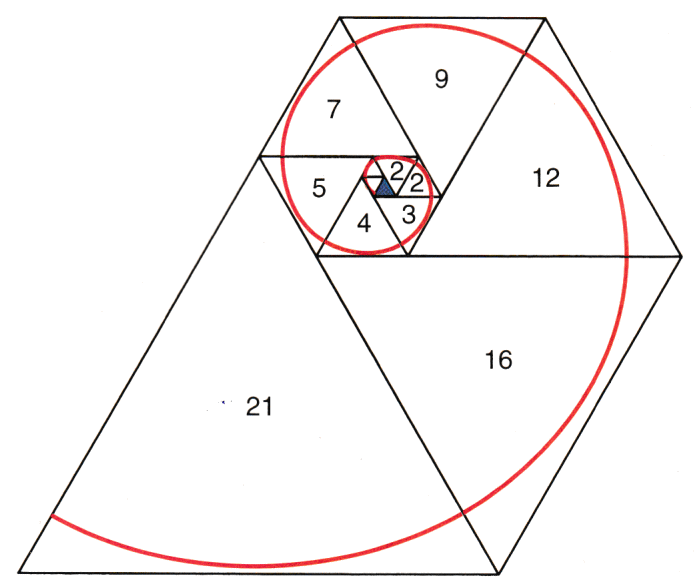
Padovan - Zahlen	1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16	Jede Zahl ist die Summe des vorletzten und des vorvorletzten.	Wenn man Dreiecke unterschiedlicher Größe spiralförmig aneinander legt, so haben die Seitenlängen der Dreiecke die Größe der Padovan - Zahlen.
Vermutung	Wähle eine beliebige ganze Zahl. Regel 1: Ist die Zahl gerade, so teile durch 2. Regel 2: Ist die Zahl ungerade, so multipliziere mit 3 und addiere 1	Am Ende immer 1	Beispiel: 11 ungerade: *3 = 33 + 1 = 34 gerade: / 2 = 17 ungerade: *3 = 51 + 1 = 52 gerade: / 2 = 26 gerade: / 2 = 13 ungerade: *3 = 39 + 1 = 40 gerade: / 2 = 20 gerade: / 2 = 10 gerade: / 2 = 5 ungerade: *3 = 15 + 1 = 16 gerade: / 2 = 8 / 2 = 4 / 2 = 2 / 2 = 1
Goldbachs Vermutung	Jede gerade Zahl > 4 ist die Summe zweier Primzahlen	6 = 5 + 1 8 = 7 + 1 10 = 7 + 3 12 = 7 + 5 14 = 11 + 3 16 = 11 + 5 = 13 + 3 18 = 13 + 5
Collatz - Folge		Iterationsfunktion, nicht eindeutig umkehrbar, z.B. T(9) = 28 und T(56) = 28

Impressum                                 Zuletzt geändert am 01.05.2015 12:21