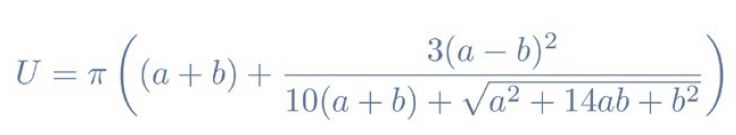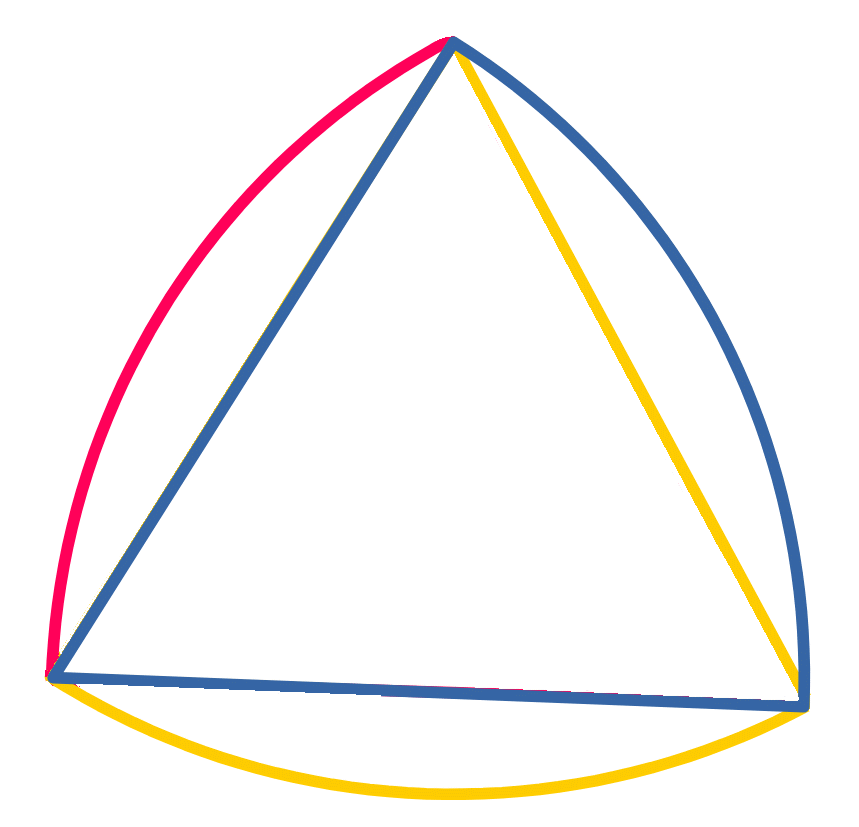zurück Home	Geometrie der Ebene
allgemeines	Notation:	Linien: kleine Buchstaben.	Punkte: große Buchstaben.	Winkel: kleine griechische Buchstaben
Elemente	Punkt	Gerade	Strahl	Strecke	Vektor
	parallel - orthogonal	Winkel	Strahlensatz	harmonische Teilung
Parallele	Parallelen sind Geraden, die in einer Ebene liegen, aber keinen gemeinsamen Punkt haben.
	5. Postulat der Elemente des Euklid	Moderne Formulierung: In einer Ebene α gibt es zu jeder Geraden g und jedem Punkt S außerhalb von g genau eine Gerade, die zu g parallel ist und durch den Punkt S geht.
Vieleck	Flächen mit n gradlinigen Begrenzungen: Dreieck Viereck: Tangenten-, Sehnen-Viereck
Kreis	A = π r2 A: Fläche r: Radius		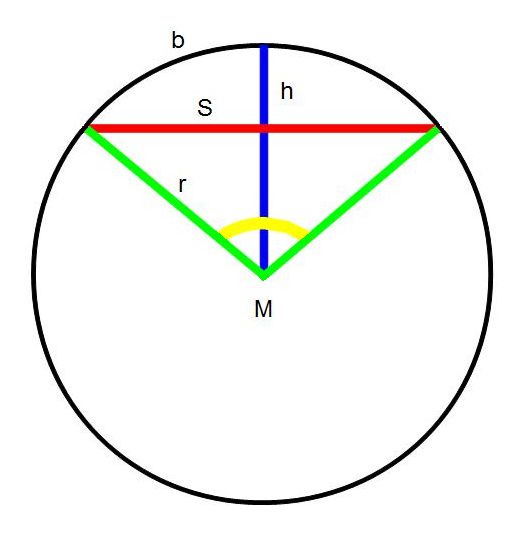S: Sehne, rot h: Höhe des Kreisabschnitts b: Bogenlänge des Kreisabschnitts r: Radius des Kreises M: Mittelpunkt des Kreises γ: Winkel des Kreissegments, gelb
Kreis und Gerade	Sehne: Sehnensatz	Sekante: Sekantensatz	Tangente: Tangenten - Sekantensatz
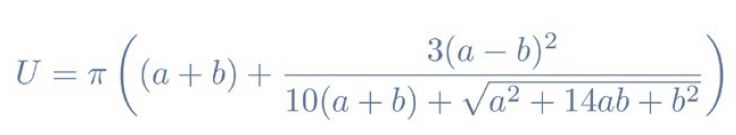
Ellipse	Menge aller Punkte definieren, bei denen die Summe der Abstände von zwei vorgegebenen Orten gleich ist. Zeichnung von ThaniosAkro [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]	Umfang einer Ellipse: Ramanujans Näherungsformel a: große Halbachse b: kleine Halbachse
Gleichdick	Reuleaux-Dreieck	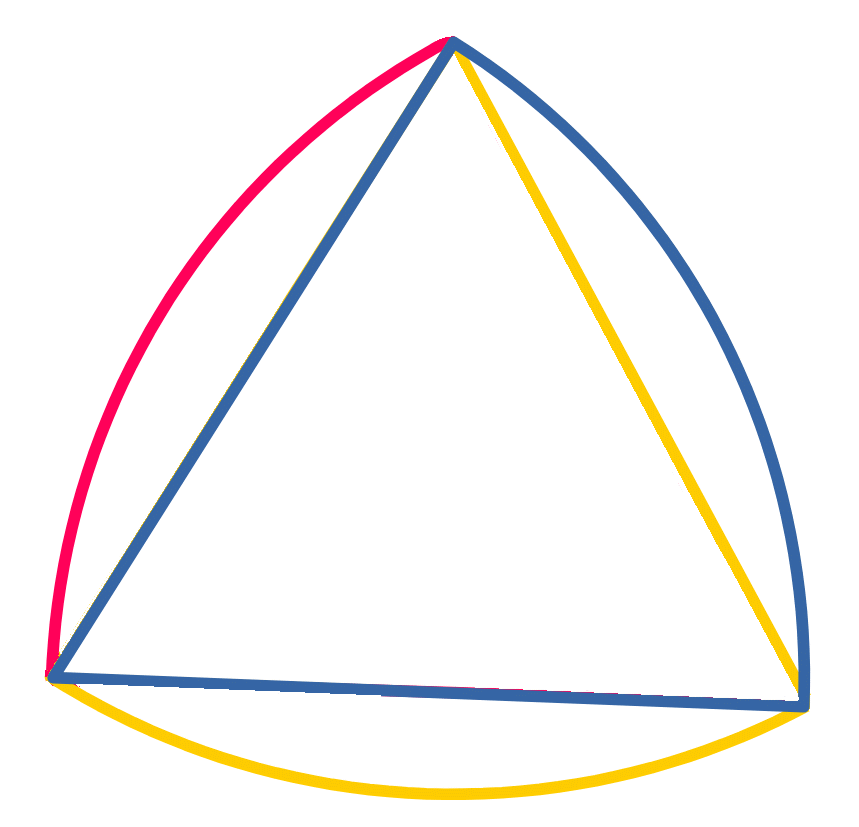Jede Seite ist ein Kreisbogen, dessen Mittelpunkt eine Dreiecks-Ecke ist. Der Durchmesser des Objektes ist in jeder Drehrichtung gleich. Formel nach Barbier: U = b * π U: Umfang B: Breite
Teil von	Geometrie		Mathematik

Impressum                           Zuletzt geändert am 28.10.2024 10:50