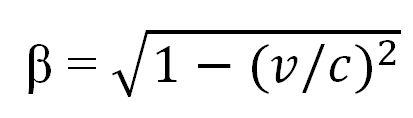
Je mehr sich die Geschwindigkeit v der Lichtgeschwindigkeit c nähert, um so kleiner wird der Zeitablauf β.
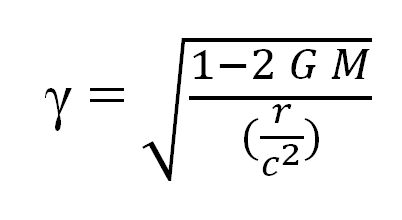
r: Radius des Himmelskörpers
M: Masse des Himmelskörpers
c: Lichtgeschwindigkeit
G: Gravitationskonstante
Teil von
| zurück Home | Relativitätstheorie | |||
| allgemeines | ||||
| spezielle Relativitätstheorie | nichts ist schneller als das Licht | Albert Einstein 1915: allgemeine Relativitätstheorie | ||
| Zeitdilatation | In einem bewegten System gehen die Uhren langsamer. | 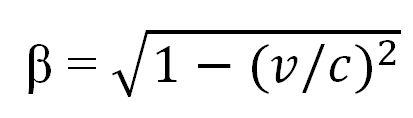 Je mehr sich die Geschwindigkeit v der Lichtgeschwindigkeit c nähert, um so kleiner wird der Zeitablauf β. |
Ein Zeitraum Δt verkürzt sich bei der Geschwindigkeit v auf den kleineren Zeitraum β * Δt | |
| allgemeine Relativitätstheorie | Albert Einstein 1915: Die Gravitation wird neu definiert. | Die Schwerkraft ergibt sich direkt aus den geometrischen Eigenschaften eines vierdimensionalen Universums. | ||
| Gravitation und Zeit | Nach der allgemeinen Relativitätstheorie verlangsamt sich der Zeitablauf in einem Gravitationsfeld. |
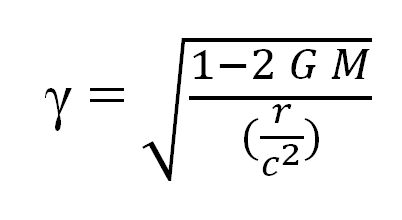 r: Radius des Himmelskörpers M: Masse des Himmelskörpers c: Lichtgeschwindigkeit G: Gravitationskonstante |
||
| vierdimensionaler Raum | Der vierdimensionale Raum vereint Raum und Zeit zu einer gemeinsamen Raumzeit. | Ein massereiches Objekt verbiegt die Raumzeit und zwingt so andere Körper auf eine gekrümmte Bahn. | ||
| schwarzes Loch | Schwarze Löcher entstehen durch die Konzentration von Masse auf kleinsten Raum. | Es wird eine Singularität bildet, in dem die Raumzeit unendlich stark gekrümmt ist. | Die Grenze zum übrigen Kosmos ist der Ereignishorizont. | |
| Ereignishorizont | Bereich eines schwarzen Lochs, in dem die Anziehung so groß ist, das nichts den Ereignishorizont überwinden kann. | Da auch kein Licht den Ereignishorizont überwinden kann, ist das schwarze Loch unsichtbar. | ||
| Äquivalenzprinzip | In der allgemeinen Relativitätstheorie sind Gravitation und Trägheit wesensgleich. | Schwere Masse (Gravitation) und träge Masse (Trägheit) sind immer gleich (Loránd Eötvös 1890). | ||
| Christoffelsche Symbole | Dienen der Beschreibung einer Parallelverschiebung im gekrümmten Raum. | Erzeugung durch partiellen Ableitungen der Metrik. | In der allgemeinen Relativitätstheorie werden sie benötigt, um die Bewegungsgleichung von Körpern zu erzeugen. Sie stellen das Gravitationsfeld dar. | |
| Feldgleichungen | Mathematische Beschreibung von Feldern einer Quelle mit Differenzialoperatoren. | In einer Feldtheorie steht in den Feldgleichungen auf einer linken Seite der Differenzialoperator, der auf das Feld einwirkt. Auf rechten Seite, der die Quelle wiedergibt. | ||
| Einsteinsche Feldgleichungen | In den Einsteinschen Feldgleichungen wird die Quelle durch den Energie-Impuls-Tensor der Materie dargestellt. | Das Feld durch Ableitungen des metrischen Tensors. | ||
| Geodäte | Eine Geodäte ist die am wenigsten gekrümmte Verbindung zwischen zwei Punkten in der Raumzeit. | In der euklidischen Geometrie ist dies eine Gerade. | Auf einer Kugel verläuft die Geodäte entlang eines Großkreises. | In einer gekrümmten Raumzeit schmiegt sich die Geodäte an die lokale Geometrie an. |
| Inertialsystem | Gleichförmig bewegte Bezugssysteme in der klassischen Physik. | In Inertsystemen haben die physikalischen Gesetze dieselbe Form wie in einem kräftefreien, ruhenden System. | ||
| Kovarianz | Kovariante Gleichungen behalten bei einer Koordinatentransformation ihre Form bei. | Allgemein kovariante Gleichungen behalten ihre Form bei sämtliche Koordinatentransformationen bei. | ||
| Lagrange-Funktion | Die Lagrange-Funktion beschreibt die Dynamik eines physikalischen Systems. | In der klassischen Mechanik kann mit der Lagrange-Funktion die Differenz von potenzieller und kinetischer Energie beschieben werden. | Daraus lassen sich Bewegungsgleichungen ableiten. | |
| Metrik | Die Metrik ist eine Vorschrift für die Berechnung von Abständen in gekrümmten Räumen. | In der allgemeinen Relativitätstheorie wird die Metrik durch einen metrischen Tensor dargestellt. | Durch den metrischen Tensor kann die Gravitation als Eigenschaft einer gekrümmten Raumzeit definiert werden. | |
| Noether-Theorem | Bei jeder Koordinatentransformationen bestehen Symmetrien für physikalische Erhaltungsgrößen. | Zur Translationssymmetrie der Zeit gehört die Erhaltung der Energie. | Wenn ein System unabhängig gegenüber Translationen und Rotationen ist, gilt die Erhaltung von Impuls und Drehimpuls. | |
| Newtonscher Grenzfall | Bei schwachen und statischen Gravitationsfeldern ergeben sich gleiche Ergebnisse nach dem Newton'schen Gravitationsgesetz und der allgemeinen Relativitätstheorie. | |||
| Tensoren | Tensoren sind eine Verallgemeinerung des Vektorbegriffs. | Tensoren werden auf Größen angewendet, die durch beliebig viele Komponenten charakterisiert sind. | Die Darstellung erfolgt i. d. R. mit Matrizen. | |
| Relativitätsprinzip | Nach der speziellen Relativitätstheorie haben alle Inertialsystemen die gleichen physikalische Gesetze. | In beschleunigten Testlaboren müssen identische Messanordnungen gleiche Ergebnisse liefern. | ||
| Riemann-Tensor | Auch Krümmungstensor, besteht aus 10 unabhängigen Komponenten. | Die Komponenten des Riemann-Tensors erhält man aus partiellen Ableitungen der Christoffel'schen Symbole. | Der Riemann-Tensor ist ein Maß für die Krümmung der Raumzeit. | |
| gravitative Rotverschiebung | Lichtteilchen verlieren etwas Energie, wenn sie aus einem starken Gravitationsfeld entkommen. | Dadurch vergrößert sich ihre Wellenlänge. | Der Stern S2 umkreist das schwarze Loch im Zentrum unserer Milchstraße. Es konnte nachgewiesen werden, sass das Licht von S2 wurde deutlich röter wurde, wenn sich der Stern dem schwarzen Loch näherte. Damit konnte die gravitative Rotverschiebung nachgewiesen werden. | |
| Unruh-Effekt | Für einen beschleunigten Beobachter füllt sich der leere Raum plötzlich mit lauter Teilchen. | Eine ruhende Person sieht davon allerdings nichts. Aus ihrer Perspektive sendet das bewegte Objekt aber Strahlung aus. | ||
| Quellen |
1.) : |
|||
Teil von |
Physik | |||
Impressum Zuletzt geändert am 30.01.2016 21:06