| zurück
Home |
Statistik |
| allgemeines |
|
| deskriptive Statistik |
graphische Darstellung |
| Korrelation |
- lineare Regression
- Maßkorrelation (Pearson - Bravais)
- Rangkorrelation (Krueger - Spearman)
- Fisher' z-Transformation
- Zufallshöchstwert
- Vertrauensgrenzen
- Differenz zweier Korrelationen
|
| Regression |
Verteilungen:
- Normalverteilung
- Binominalverteilung
- t - Verteilung
- F -Verteilung
- Chi – Quadrat - Verteilung
- schiefe Verteilung
- Prüfung einer Verteilung
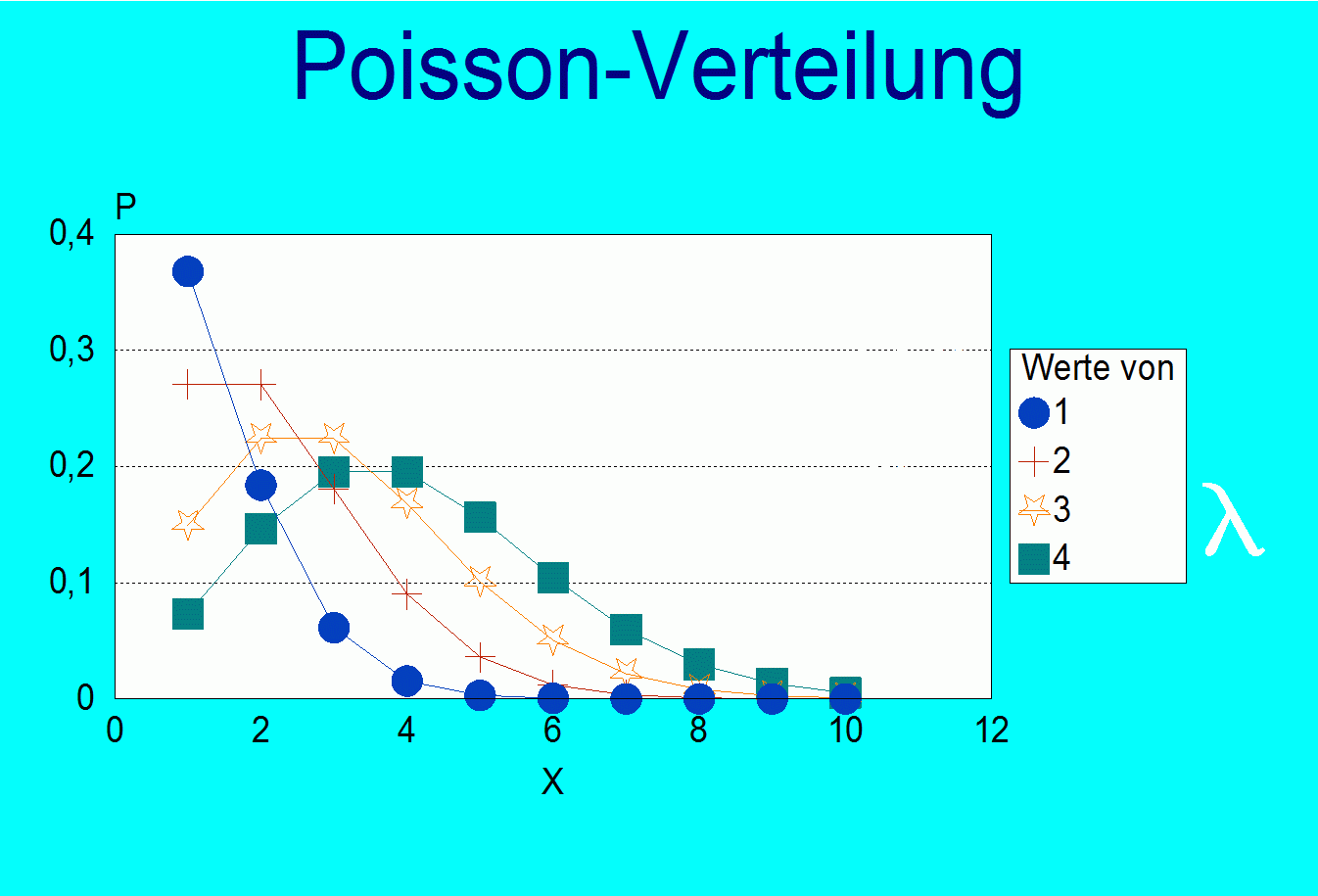
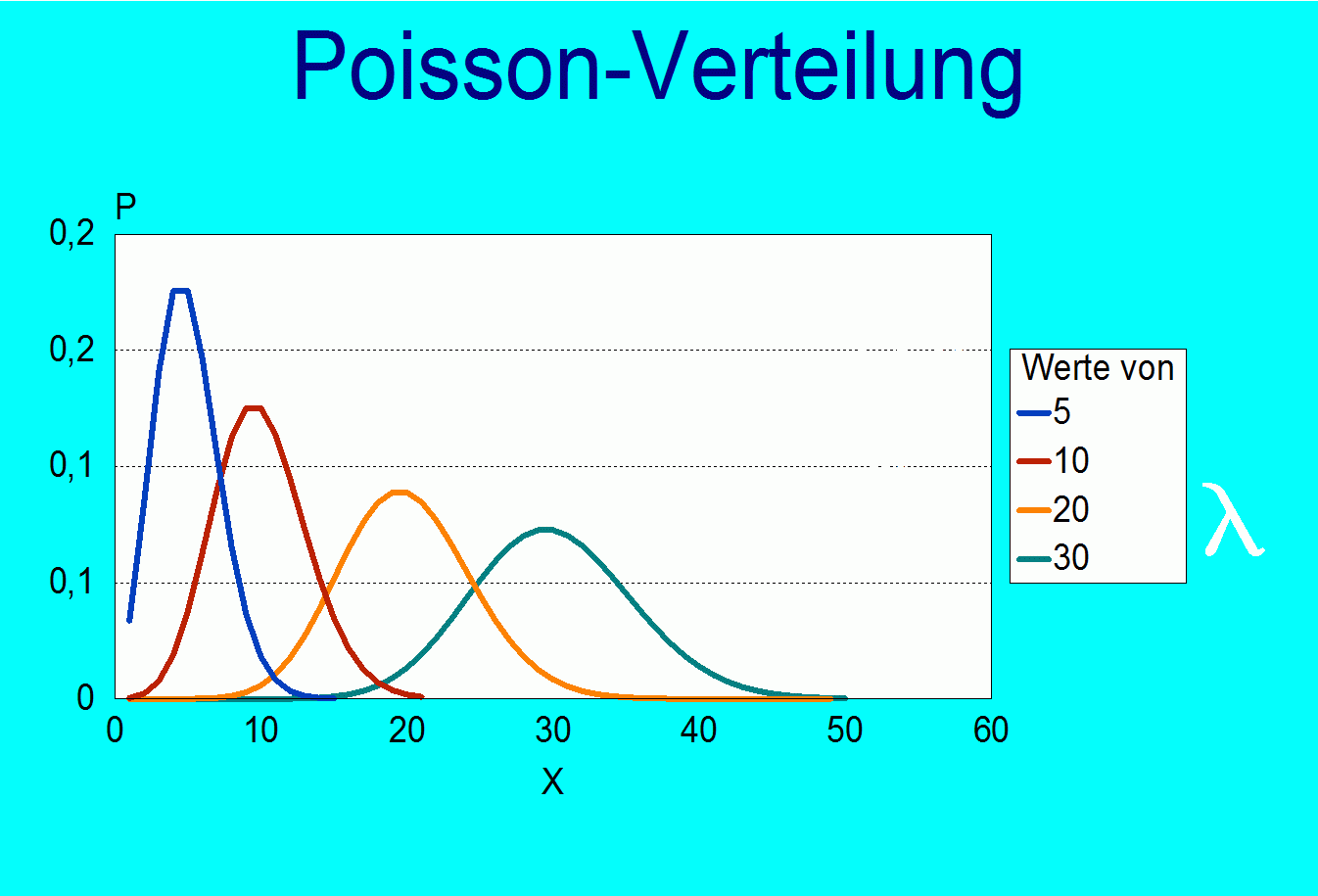
- Poisson - Verteilung
|
 |
 |
 |
| statistische Tabellen |
Chi-Quadrat |
Konfidenz |
| Prüfstatistik |
Signifikanz: Bonferroni - Korrektur |
Mittelwertunterschiede |
non parametrische Teste |
| Testung von Häufigkeitsunterschieden |
Kontingenz |
Varianzanalyse |
Faktorenanalyse |
Missing - Data - Probleme |
| klinische Statistik |
Studie |
Phasen |
Dosiseskalation |
Tumor - Statistik
Endpunkte |
| Metaanalyse |
Bias |
Survival - Statistik |
multivariate Analyse |
Altersstandardisierte Rate |
| Simpsons Paradox |
| Arm |
lebt |
tot |
Statistik |
| A |
40 |
40 |
50% |
| B |
32 |
48 |
40% |
Arm A besser als Arm B |
Nur Männer
| Arm |
lebt |
tot |
Statistik |
| A |
36 |
24 |
60% |
| B |
14 |
6 |
70% |
Arm B besser als Arm A |
Nur Frauen
| Arm |
lebt |
tot |
Statistik |
| A |
4 |
16 |
20% |
| B |
18 |
42 |
30% |
Arm B besser als Arm A |
Nach Aufteilung der Gesamtgruppe kehrt sich das Ergebnis um |
A,B,C,D: Werte der 1. Tabelle
a,b,c,d: Werte der 2. Tabelle
a',b',c',d': Werte der 3. Tabelle |
A = a + a'
B = b + b'
C = c + c'
D = d + d' |
Simpsons Paradoxon wenn
A / B > C / D und
a / b < c / d und
a' / b' < c' / d' |
Ungleichungen dürfen nicht addiert werden! |
| Test-Statistik |
Sensitivität: Prozent positiv bei Infektion |
Spezifität: Prozent infiziert bei positivem Test |
positive Vorhersagewert: Richtig positiv getestet durch alle positiv getesteten |
negativer Vorhersagewert: Richtig negativ getestet durch alle negativ getesteten |
| Vortest-Wahrscheinlichkeit |
Das Ergebnis des positiven und negativen Vorhersagewertes ist vom Prozentsatz der Infizierten abhängig. |
Test-Beispiel:
Sensitivität 70 %
Spezifität 95 % |
Bei 70 % der Infizierten ist der Test positiv
bei 30 % der
Infizierten ist der Test negativ |
Bei 95 % der positiv getesteten liegt eine Infektion vor.
Bei 5 % der positiv getesteten Licht keine Infektion vor. |
Population mit 3 % Infizierten:
30 von 1000 Personen sind infiziert
970 Personen sind nicht infiziert |
21 von 30 werden richtig positiv getestet
49 von 970 werden falsch positiv getestet
9 von 30 werden falsch negativ getestet
921 von 970 werden richtig negativ getestet |
Positiver Vorhersagewert: 21/(21 + 49) = 70 %
negativer Vorhersagewert 921/(921 + 9) = 99 % |
In einer Population mit niedriger Prävalenz ist der positive Vorhersagewert gering, der negative Vorhersagewert ist hoch. |
Population mit 80 % Infizierten:
800 von 1000 Personen sind infiziert
200 Personen sind nicht infiziert |
560 von 800 werden richtig positiv getestet
10 von 200 werden falsch positiv getestet
240 von 800 werden falsch negativ getestet
190 von 200 werden richtig negativ getestet |
Positiver Vorhersagewert: 560/(560 + 10) = 98 %
negativer Vorhersagewert 190/(190 + 240) = 44 % |
Bei hoher Prävalenz ist der positive Vorhersagewert hoch und deren negative Vorhersagewert gering. |
| Informatik |
|
| Quellen |
1.) Stengel D, et al.:
Statistik und Aufbereitung klinischer Daten.
Thieme 2010
2.) Statistische Bundesamt
|
Teil von |
Mathematik |
|
|
 |
|



