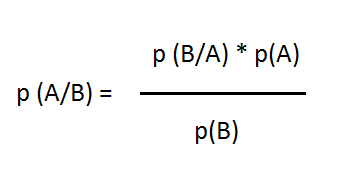| zurück
Home |
Tumor - Statistik |
| Mortalität, Inzidenz |
Zur Beschreibung von Erkrankungshäufigkeit und Sterblichkeit sind exakte Definitionen notwendig. |
| Studien |
Studien sind die wichtigste Erkenntnisquelle in der Onkologie. |
| Metaanalyse |
MOOSE (14) |
Meta-analyses Of Observational Studies in Epidemiology guidelines |
| Register |
Register sammeln Daten ohne eigentliche Fragestellung. |
Dadurch sind flächendeckende, epidemiologische Abschätzungen möglich. |
| Verlaufsstatistik |
Die Wirksamkeit einer Therapie zeigt sich in der Regel am Heilungsverlauf. |
Zur quantitativen Auswertung wird ein Startpunkt, z.B. der Therapiebeginn und Endpunkt, z.B. Tod festgelegt. |
| Endpunkte |
Neben dem Versterben gibt es eine Reihe von Endpunkten, die in der Literatur mit Abkürzungen gekennzeichnet wird. |
| Remission |
Rückbildung eines Tumor unter einer Therapie, z.B. Strahlentherapie |
| RR |
Bei der Analyse verschiedener Faktoren wird oft ein RR, ein relatives Risiko angegeben. |
| Evidenz |
| Methoden zur Gewinnung von Evidenz |
Randomisierte Studien |
- adaptives Design, z.B. Bayesian adaptive Randomisation
- pragmatische Studie, z.B. Kontrollarm = übliche Therapie
|
| Beobachtungsstudien |
- prospektive Kohorten
- retrospektive Kohorten
- Case-Control-Studien
- Cross-Sectional-Studien
- Analyse aggregierter Daten: Register, Versicherungen
|
| Methoden zur Synthese von Evidenz |
Metaanalyse |
systematischer Review |
Mathematisches Modell |
in Anlehnung an (2) |
| Level of Evidence |
Die Vertrauenswürdigkeit von Aussagen wird durch eine Skala der Glaubwürdigkeit (Evidenz) ausgedrückt. |
| Vertrauensbereich |
Bei jeder Statistik weicht der ermittelte Wert ein wenig von dem wahren Wert der Grundgesamtheit ab. |
Dieser Schätzfehler wird bei zunehmender Fallzahl geringer. |
Der Vertrauensbereich kennzeichnet die Spanne, innerhalb der der wahre Wert mit einer bestimmten Wahrscheinlichkeit liegt. |
| Bias |
Systematische Fehler lassen sich auch durch sehr große Stichproben nicht vermindern. |
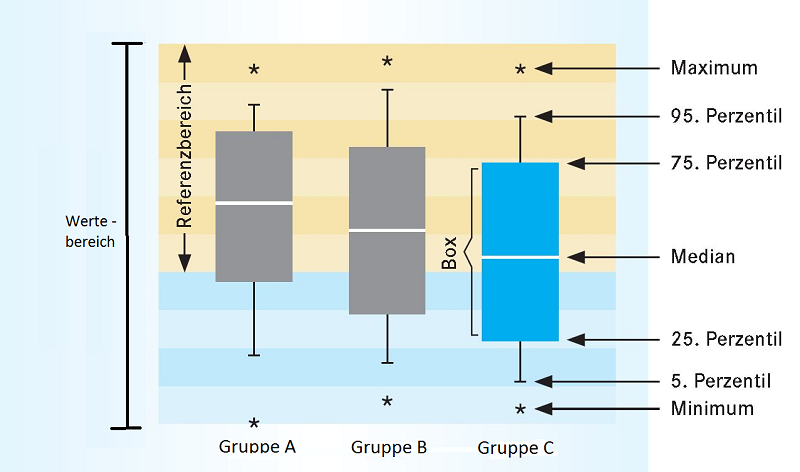
| Box - Whisker - Plot |
Der Box-Whisker-Plot stellt einen Wertebereich in komprimierter Form dar. Unterschiede von Gruppen lassen sich auf einen Blick erkennen.
 |
| Bedingte Wahrscheinlichkeit |
Thomas Bayes hat eine Formel entwickelt, um die
Wahrscheinlichkeit p (A/B) eines Ereignisses B zu berechnen, wenn das Ereignis B eingetreten ist:
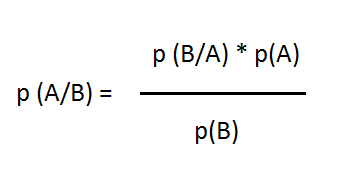
p(A): Wahrscheinlichkeit, dass A eintritt
p(B): Wahrscheinlichkeit, dass B eintritt
p(B/A): Wahrscheinlichkeit, dass B eintritt, wenn A bereits eingetreten ist
p(A/B): Wahrscheinlichkeit, dass A eintritt, wenn B bereits eingetreten ist |
| mathematische Statistik |
deskriptive Statistik, Prüfstatistik, Simpsons Paradox, Test-Statistik, Vortest-Wahrscheinlichkeit |
| Biometrie |
GMDS, Medizinische Informatik, Medizinische Biometrie, Lebenserwartung, Epidemiologie, Krankenversicherung, Medizinische Dokumentation, Medizin - Software, Health Monitor |
Teil von |
allgemeine Onkologie |
Onkologie |
| Quellen |
1.) Kaplan EL, Meier P:
Non parametric estimation from incomplete observations.
J Am Stat Assoc 53(1958):457–481
2.) Kopsell TD:
Epidemiologic Methods Studying the Occurrence of Illness.
Oxford University Press, New York 2003.
3) Hahn OM, Schilsky RL:
Randomized controlled trials and comparative effectiveness research.
J Clin Oncol 30(2012):4194-4201
4.) Motulsky H:
Essential Biostatistics: A Nonmathematical Approach.
Oxford Univerity Press 2016
5.) Clauss G, Ebner H:
Grundlagen der Statistik.
Verlag Harri Deutsch, Frankfurt a.M. und Zürich, 1971
6.) KreyszigE :
Statistische Methoden und ihre Anwendungen.
Vandenhoeck und Ruprecht, Göttingen 1967
7.) Weber E:
Grundriß der biologischen Statistik.
Gustav Fischer Verlag Stuttgart, 1972
8.) Pfanzagl J:
Allgemeine Methodenlehre der Statistik I und II.
Sammlung Göschen; Walter de Gruyter, Berlin 1972
9.) van der Waerden BL:
Mathematische Statistik.
Springer-Verlag Berlin, Göttingen, Heidelberg 1957,
neu aufgelegt 1972
10.) Morgenstern D:
Einführung in die Wahrscheinlichkeitsrechnung und Mathematische Statistik.
Springer-Verlag, Berlin, Göttingen, Heidelberg, 1964
11.) Rbnyi A:
Wahrscheinlichkeitstheorie mit einem Anhang über Informationstheorie.
VEB Deutscher Verlag der Wissenschaften, Berlin 1966
12.) Bauer H:
Wahrscheinlichkeitstheorie und Grundzüge der Maßtheorie.
Walter de Gruyter Berlin 1968
13.) Sachs L:
Statistische Auswertungsmethoden.
Springer, Berlin, Göttingen, Heidelberg, New York 1969
14.) Stroup DF, Berlin JA, Morton SC, et al.:
Meta-analysis of observational studies in epidemiology: a proposal for reporting. Meta-analysis Of Observational Studies in Epidemiology (MOOSE) group.
JAMA 2000;283:2008–12.
|
 |