| zurück
Home |
Zahlen |
| allgemeines |
|
| Zahl |
Aus Ziffern zusammengesetzte Darstellung eines nummerischen Wertes |
Ziffer |
Symbolische Darstellung eines abzählbar ganzen Wertes |
| Ziffernsysteme |
System zur Darstellung von Zahlen mit Ziffern und Sonderzeichen |
| Dezimalsystem |
zehn Ziffern |
| Dualsystem |
2 Ziffern 0 und 1 |
| Hexadezimalsystem |
16 Ziffern, 0-9, a-7 |
| BCD-Zahlen |
Binärsystem, welches nur 10 Ziffern nutzt. Für Finanzberechnungen. |
| Oktalsystem |
8 Ziffern 0 bis 7 |
|
| benfordsches Gesetz |
In großen Datensätzen treten die Ziffern nicht gleich häufig auf. In 30,1% ist eine 1 an erster Stelle, nur 4,6% eine 9. |
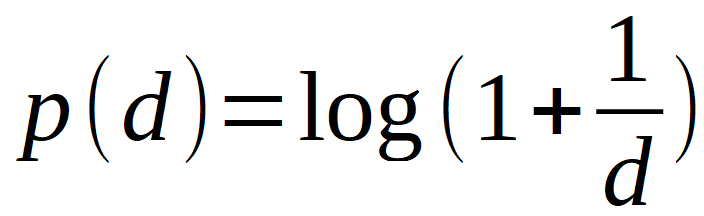
p: Wahrscheinlichkeit
d: Ziffer |
| Dezimalbruchentwicklung |
Ermittlung eines Zahlenwertes aus den Ziffern und deren Multiplikatoren, z.B.: |
987,654 = 9 * 102 + 8 * 101 + 7 * 100 + 6 * 10-1 + 5 * 10-2 + 4 * 10-3 |
| numerisches Rechnen |
Nomographie |
| elementare Zahlentheorie |
Peano - Axiome |
| 1 |
o ist eine natürliche Zahl |
| 2 |
Jede natürliche Zahl hat eine natürliche Zahl als Nachfolger |
| 3 |
0 ist kein Nachfolger einer natürlichen Zahl |
| 4 |
Natürliche Zahlen mit gleichem Nachfolger sind gleich |
| 5 |
Enthält X die 0 und mit jeder natürlichen Zahl n auch deren Nachfolger, so bilden die natürlichen Zahlen eine Teilmenge von X. |
|
| natürliche Zahlen |
1 , 2 , 3 , .... . |
Jede natürliche Zahl ist ein Produkt von Primzahlen. |
| rationale Zahlen |
positive und negative Dezimalzahlen |
können addiert, subtrahiert, multipliziert und dividiert werden: Sie bilden einen Körper |
Rationale Zahlen sind unvollständig, z.B. √2 ist nicht darstellbar. |
| irrationale Zahlen |
Folge rationaler Zahlen, die zu einem Grenzwert konvergieren. |
| π |
3,14159 26535 89793 23846 26433 83279 50288 41971 |
| e |
2,3025850929940456840179914546844 |
| reelle Zahlen |
Umfassen die rationalen Zahlen und die irrationalen Zahlen. |
|
| imaginäre Zahlen |
i2 = -1 |
Die Einführung der imaginären Zahl i war notwendig, um z.B. die Gleichung x2 + 1 = 0 zu lösen |
Quaternionen, Oktonionen |
| Primzahlen |
natürliche Zahlen ohne Teiler. |
Jede natürliche Zahl ist ein Produkt von Primzahlen. |
Jede ungerade Zahl ist die Summe dreier Primzahlen |
| Goldbach'sche Vermutung: Jede gerade Zahl > 4 kann als Summe zweier Primzahlen ausgedrückt werden |
| Zufallszahlen |
Blum-Blum-Shub-Generator |
s0 = s2 mod n (Rest nach Teilung durch n)
si+1 = si2 mod n |
Die Parameter s und n dürfen keinen gemeinsamen Teiler haben. |
| N muss das Produkt zweier Primzahlen sein, die sich beide in der Form 4K +3 darstellen lassen. |
Anwendung in der Kryptologie. |
| Fibonacci - Zahlen |
0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144, 233 , 377 .... |
Jede Zahl ist die Summe ihrer zwei Vorgängerinnen. |
| Pascalsches Dreieck |
Beginn mit 1.
Jede Zahl ist die Summe der beiden Zahlen darüber.
| |
|
|
|
1 |
|
|
|
|
| |
|
|
1 |
|
1 |
|
|
|
| |
|
1 |
|
2 |
|
1 |
|
|
| |
1 |
|
3 |
|
3 |
|
1 |
|
| 1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
Teil von |
Mathematik |
 |